5 树
目录
[5] 树
树的理论东西和概念挺多,相应的计算也多,考试比较常考,所以会专门弄出一些地方来写这些东西
基本概念
树的定义
树是 n 个结点的有限集
基本术语
- 空树:n=0
- 根结点、分支结点、叶子结点
- 非空树的特性
- 子树
结点之间的关系描述
祖先结点
子孙结点
双亲结点
兄弟结点:和该节点统一深度的节点
路径
路径长度
(注意:数的连线是有方向性的,只能从上往下,不能从下往上,即不能求子节点到父节点的距离)
结点、树的属性描述
结点的层次(深度):从上往下
结点的高度:从下往上
树的高度:总共多少层
结点的度:有几个孩子
树的度:各结点的度的最大值
有序树、无序树
森林
树的性质
树中的结点数等于所有结点的度数之和加 1。
度为
m的树第i层上至多有m^i-1个结点度为
m的数、m叉数的区别对比项 度为 m的树m叉树m的定义m为各结点的度的最大值(树的度)每个结点最多只能有 m个孩子的结点的度要求 至少有一个结点度 =m允许所有结点的度 <m最少节点数 一定是非空树,至少有 m+1个结点,可为无限节点可以是空树,节点优先 第 m层节点数至多有 m^(i-1)个结点至多有 m^(i-1)个结点节点数 高度为 h、度为m的树至少有h+m-1个结点高度为 h的m叉树至多有(m^h-1)/(m-1)个结点;至少有h个结点具有 n个结点的m叉树,最小高度为 1og~m~(n(m-1)+1)结点 结点无左、右之分 结点有左、右之分
[5] 树
树的存储结构
[5-1] 树-双亲表示法
顺序存储
- 每个结点中保存指向双亲的指针
数据域:存放结点本身信息 双亲域:指示本结点的双亲(父节点?)结点在数组中的位置
c
#define MAX_TREE_SIZE 100 //树中最多结点数
typedef struct{ //树的结点定义
ElemType data;
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MAX_TREE_SIZE]; //双亲表示
int n; //结点数
}PTree;- 增:新增数据元素,无需按逻辑上的次序存储(需要更改结点数 n)
- 删(叶子结点)(需要更改结点数 n)
- 将伪指针域设置为-1
- 用后面的数据填补
- 查询
- 优点-查指定结点的双亲很方便
- 缺点-查指定结点的孩子只能从头遍历,空数据导致遍历更慢
[5-2] 树-孩子表示法
顺序+链式
孩子链表:把每个结点的孩子结点的地址信息排列起来,看成是一个线性表,用单链表存储,则 n 个结点有 n 个孩子链表(叶子的孩子链表为空表)。而 n 个头结点又组成一个线性表,用顺序表(含 n 个元素的结构数组)存储。
c
typedef struct{
int child; // 孩子结点在数组中的位置
struct CTNode *next; // 下一个孩子
}CTNode;
typedef struct{
ElemType data; // 数据
struct CTNode *firstChild; // 指向一个链表,表头为第一个孩子的信息
}CTBox;
typedef struct{
CTBox nodes[MAX_TREE_SIZE];
int n, r; // 结点数和根的位置
}CTree;[5-4] 孩子兄弟表示法*
链式
最推荐的实现方法
c
typedef struct{
ElemType data; //数据域
//第一个孩子和右兄弟指针, *firstchild 看作左指针,*nextsibling看作右指针
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;AP>树&森林&二叉树的转换
本质:森林中各个树的根结点之间视为兄弟关系
将树转换成二叉树:
- 加线:在兄弟之间加一连线
- 抹线:对每个结点去除其与孩子之间的关系(第一孩子除外)
- 旋转:以树的根结点为轴心,顺时针转 45 度 (兄弟相连留长子)
树:A(B(EFG)CD(HI))
=>
转化为二叉树:A(B(E(F(G))C(D(H(I)))))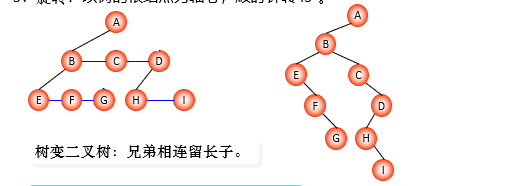
[5] {4} 树的遍历
- 树的遍历
- 先根遍历:若树非空,先访问根结点,再依次对每棵子树进行先根遍历;(与对应二叉树的先序遍历序列相同)
c
void PreOrder(TreeNode *R){
if(R!=NULL){
visit(R); //访问根节点
while(R还有下一个子树T)
PreOrder(T); //先跟遍历下一个子树
}
}- 后根遍历:若树非空,先依次对每棵子树进行后根遍历,最后再返回根节点;(与对应二叉树的中序遍历序列相同)
c
void PostOrder(TreeNode *R){
if(R!=NULL){
while(R还有下一个子树T)
PostOrder(T); //后跟遍历下一个子树
visit(R); //访问根节点
}
}- 层序遍历(队列实现):
若树非空,则根结点入队; 若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队; 重复以上操作直至队尾为空;
[5] {4} 森林的遍历
- 森林的遍历
- 先序遍历:等同于依次对各个树进行先根遍历;也可以先转换成与之对应的二叉树,对二叉树进行先序遍历;
- 中序遍历:等同于依次对各个树进行后根遍历;也可以先转换成与之对应的二叉树,对二叉树进行中序遍历;
